
이전 포스트인 알고리즘 시리즈 - 시간 복잡도에서는 알고리즘의 성능을 파악하는 척도 중 하나인 시간복잡도와 big-O에 대해서 공부해봤습니다. 시간 복잡도란 문제를 해결하는데 걸리는 시간과 입력의 함수 관계 로 문제에 적합한 자료구조와 그에 따른 알고리즘에 영향을 받으며 알고리즘의 수행 시간은 동일 크기의 다양한 입력에 의해 달라질 수 있다.
| 자료 구조 | 접근 | 검색 | 삽입 | 삭제 | 비고 |
|---|---|---|---|---|---|
| 배열 | 1 | n | n | n | |
| 스택 | n | n | 1 | 1 | |
| 큐 | n | n | 1 | 1 | |
| 연결 리스트 | n | n | 1 | 1 | |
| 해시 테이블 | - | n | n | n | 완벽한 해시 함수의 경우 O(1) |
| 이진 탐색 트리 | n | n | n | n | 균형 트리의 경우 O(log(n)) |
| B-트리 | log(n) | log(n) | log(n) | log(n) | |
| Red-Black 트리 | log(n) | log(n) | log(n) | log(n) | |
| AVL 트리 | log(n) | log(n) | log(n) | log(n) | |
| Bloom Filter | - | 1 | 1 | - | 거짓 양성이 탐색 중 발생 가능 |
위 표는 자료구조 작업별 복잡도 로써 자료구조의 특성에 따라 작업별 시간복잡도가 다름을 알 수 있으며 이번 포스트에서는 상대적으로 입문자 레벨 (참조 - JavaScript 알고리즘 및 자료 구조)에 속하는 아래 데이터 구조에 대해 공부해보겠습니다.
- 연결 리스트
- 이중 연결 리스트
- 큐
- 스택
- 해시 테이블
- 힙
- 우선순위 큐
자료구조란
자료구조란 데이터 값의 모임, 데이터 간의 관계 그리고 데이터가 사용할 수 있는 함수로써, 특정 문제를 해결하기 위한 추상화된 모델링(자료구조)은 시간 복잡도와 공간 복잡도를 줄여주는 효과가 있으며 그에 따라 효율적인 알고리즘을 수행할 수 있다. 프로그램을 설계하거나 문제해결 과정을 설계할때, 우선적으로 어떤 자료구조로 모델링할지 고려되야하며 자료구조가 선택되면 적용할 알고리즘의 폭은 상대적으로 좁혀지기 때문에 그 안에서 복잡도를 분석해가며 알고리즘을 선택하면 되겠다.
자료구조 종류
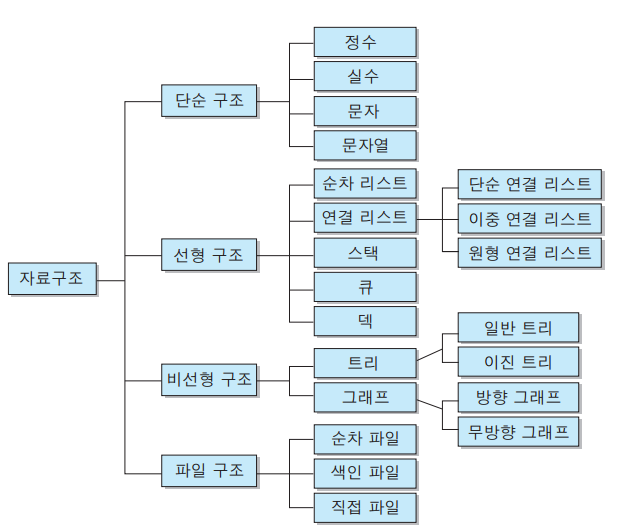
자료구조는 위 사진에서 볼수 있듯이 단순 / 선형 / 비선형 / 파일 구조로 구분되며 알고리즘 문제풀이에서 많이 사용되는 구조는 선형 / 비선형 구조이다.
선형 구조
한 종류의 데이터가 선처럼 길게 나열된 자료구조로써, 데이터 요소에 랜덤 접근여부에 따라서 랜덤 접근 가능 자료구조 - 배열, 해시 / 랜덤 접근 불가능 자료구조 - 스택, 큐, 데크, 링크드 리스트로 구분된다.
선형 구조의 자료 탐색법으로는 아래와 같다.
- 순차 탐색
- 이분 탐색
비선형 구조
선형 자료구조가 아닌 모든 자료구조로써, 사전적인 정의로 i 번째 값을 탐색한 뒤의 i+1이 정해지지 않은 구조를 의미한다. 비선형 자료구조의 종류와 간략한 정의는 아래와 같다.
- 그래프
- 꼭지점과 꼭지점을 있는 변으로 구성
- 방향 그래프, 무방향 그래프: 변이 방향성을 갖는지 아닌지에 따라 그래프의 유형을 구분할 수 있으며 무방향 그래프는 순환이 없는 그래프이고, 방향 그래프는 변의 방향이 보통 부모를 가리키도록 구현된 그래프이다.
- 트리
- 뿌리와 뿌리 또는 다른 꼭지점을 단 하나의 부모로 갖는 꼭짓접들로 이루어진 구조
- 부모 자식 관계는 변으로 표현된다.
- 트리의 종류는 연결된 자식의 개수에 따라 구분되는데 일반적으로 1개의 자식을 갖는 구조를 단순 일반 트리, 자식이 최대 2개인 트리를 이진 트리라고 한다.
- 힙 또한 이진 트리의 한 종류로 이진 트리에 특성을 부여한 것이라 할 수 있다.
마치며
이후 포스트 부터는 선형 및 비선형 구조의 각 자료구조에 대해 순서대로 다뤄보겠습니다.