ProgrammingAlgorithm

알고리즘 시리즈 - 시간 복잡도

알고리즘 성능과 Big-O

, , , , ,

알고리즘

알고리즘 개요

지난 포스트인 알고리즘 시리즈 - 시작에서는 우리는 알고리즘을 특정 문제를 해결하기 위한 일련의 계산과정으로 입력, 출력 그리고 계산과정 이 존재한다고 정의했었습니다. 또한 해결해야하는 문제의 특성에 따라 사용하기에 적합한 데이터 형태가 다르며 어떤 데이터 형태와 알고리즘 구조를 설계했느냐에 따라서 알고리즘 성능 분석 기준 중 시간복잡도와 공간복잡도 또한 달라집니다. 이번 포스트에서는 그중에 하나인 시간 복잡도에 대해서 공부해보겠습니다.

시간 복잡도

시나리오

A라는 지점에서 B 지점을 가야한다고 상상해보자. B 지점은 처음 가는 곳이며 버스를 타고 가야할지, 지하철을 타고 가야할지 그리고 대중교통 선택했다면 어떤 버스를 또는 지하철을 타고 가야하는지 조차 정보가 없다. 네이버맵에서 경로 검색 후 지하철을 타기로 했다. 추천 노선은 총 2개이고, 추천 경로는 총 5개이며 모두 경험이 없는 경로여서 어떤 경로를 선택할지 일일히 탐색해봐야 한다. (경로 탐색중…) 5개의 경로를 모두 탐색했고 그 중 1번의 환승임에도 불구하고 가장 빠르게 도착하는 경로를 선택했다.

시간 복잡도란…

위와 같은 경로 탐색의 시간이 바로 시간 복잡도 이다. 위 시나리오 처럼 전혀 데이터가 없어 모든 추천경로를 탐색한 후 비교 분석을 통해 선택한다면 시간은 추천경로의 개수만큼 늘어날 것이고, 만약 개중 데이터가 있는 경로가 있었다면 그중 선택함으로써 추천경로 모두를 탐색하지 않아도 됐을 것이다.

즉, 시간 복잡도란 문제를 해결하는데 걸리는 시간과 입력의 함수 관계 로써, 같은 결과를 내는 다수의 알고리즘이 있다면 가능한 시간이 적게 걸리는 다시말해 시간 복잡도가 낮은 알고리즘이 좋은 알고리즘이라고 판단할 수 있겠다. 기본적인 연산을 수행하는데에 고정된 시간이 걸릴 때, 알고리즘에 의해서 수행되는 기본 연산의 개수를 세어 예측할 수 있다. 알고리즘의 수행 시간은 동일 크기의 다양한 입력에 의해 달라질 수 있기 때문에, 가장 많이 쓰이는 최악의 시간 복잡도의 알고리즘 시간을 T(n)이라고 했을 때, 이것은 크기 n의 모든 입력에 대해 걸리는 최대의 시간으로 정의할 수 있다.

시간 복잡도의 종류

  1. Every-Case Time Complexity ( 𝑇(𝑛) )
    • 입력 크기 n 이 입력됐을 때, 알고리즘이 연산을 수행하는 횟수
    • 입력 크기에만 종속되며, 어떤 입력값이 들어오더라도 일정하다.
  2. The Worst Case Time Complexity( 𝑊(𝑛) )
    • 입력크기 n 이 주어졌을 때, 알고리즘이 연산을 수행하는 최대 횟수
    • 입력크기와 입력값 모두에 종속되며, 단위연산이 수행되는 횟수가 최대인 경우 선택
  3. The Best Case Time Complexity ( 𝐵(𝑛) )
    • 입력크기 n 이 주어졌을 때, 알고리즘이 연산을 수행하는 최소 횟수
    • 입력크기와 입력값 모두에 종속되며, 단위연산이 수행되는 횟수가 최소인 경우 선택
  4. The Average Case Time Complexity ( 𝐴(𝑛) )
    • 입력크기 n 이 주어졌을 때, 알고리즘이 연산을 수행하는 평균 횟수
    • 입력크기와 입력값 모두에 종속되며, 모든 입력에 대해서 단위연산이 수행되는 기대치

점근적 분석법

점근적 분석법이란 입력되는 데이터의 크기에 따라 수행 시간간과 공간이 얼마나 차지하는지 알아보는 탐색법으로써, 주어진 데이터의 형태나 실험을 수행하는 환경 또는 실험에 사용한 시스템의 성능 등의 요소에 의해 공평한 결과가 나오기 힘들고, 그 비교가 항상 일정하지 않기 때문에 필요하다.

시간복잡도를 나타내는 점근적 분석법의 표기법으로는 아래와 같으며 주로 최악의 경우인 빅오 표기법 (Big-O Notation) 을 사용하는데 그 이유는 평균의 경우를 사용하면 그 기준을 맞추기 까다롭고 모호할 수 있으며 최악의 경우를 사용하면 “아무리 나빠도 다른 알고리즘 보다는 같거나 좋다.” 라는 비교분석을 따르면 평균에 가까운 성능을 예측하기 쉽기 때문이다.

  • 최상의 경우 : 오메가 표기법 (Big-Omega(Ω) Notation)
  • 평균의 경우 : 세타 표기법 (Theta(θ) Notation)
  • 최악의 경우 : 빅오 표기법 (Big-O Notation)

Big-O

  • 시간 복잡도에 가장 큰 영향을 미치는 차항으로 시간복잡도를 나타내는 것으로 알고리즘 실행 시간의 상한선을 나타낸 표기법이다.
  • Big-O 표기법 이라 하며 O(f(n)) 과 같이 표기한다. (O는 order 라고 읽는다.)
1
2
3
4
5
6
7
1                        # O(1): 상수

T(n)=2n                  # O(n): n이 가장 큰 영향을 미친다.

T(n)=2n^5+3n^4+n^3+n^2+1 # O(n5): n^5이 가장 큰 영향을 미친다

T(n)=3n^2+2n+1           # O(n2): n^2이 가장 큰 영향을 미친다.

Big-O 표기법의 종류

※ 여기서 n이란 입력되는 데이터를 의미합니다.

f(n) Name 비고
1 Contant (상수) Operation push and pop on Stack
log n Logarithmic (로그) Binary Tree
n Linear (선형) for loop
n log n Log Linear (선형 로그) Quick Sort, Merge Sort, Heap Sort
n2 Quadratic (제곱) Double for loop, Insert Sort, Bubble Sort, Selection Sort
2n Exponential (지수) Fibonacci Sequence

Big-O 표기법의 설명

  1. O(1)
    • 상수 시간
    • 문제 해결을 위해 오직 한 단계만 거침
    • 입력되는 데이터 양과 상관없이 일정한 시간 동안 실행
  2. O(log n)
    • 로그 시간
    • 입력 데이터의 크기가 커질수록 처리 시간이 로그(log) 만큼 짧아지는 알고리즘
    • 입력값 n이 주어졌을때, 문제를 해결하는데 필요한 단계들이 연산마다 특정요인에 의해 줄어듬
    • 입력 데이터 10 투입되면 시간은 2배가 걸림
  3. O(n)
    • 직선적 시간
    • 문제를 해결하기 위한 단계의 수와 입력 데이터의 크가 n이 1:1 관계를 가지는 알고리즘
    • 예) 1차원 for loop
  4. O(n log n)
    • 선형 로그 시간
    • 입력 데이터의 크기가 커질수록 처리 시간이 로그(log) 만큼 늘어나는 알고리즘
    • 예) 입력 데이터 10 투입되면 시간은 20배가 걸림
    • 대표적 알고리즘: 병합 정렬 알고리즘, 퀵 정렬 알고리즘
  5. O(n2)
    • 제곱 시간
    • 입력 데이터의 크기에 따라 걸리는 시간은 제곱에 비례
    • 이중 루프 내에서 입력 데이터를 처리하는 경우에 나타남
    • n 값이 커지면 실행 시간이 감당할 수 없을 정도로 늘어남
    • 문제를 해결하기 위한 단계의 수에 해당
    • 대표적 알고리즘: 버블 정렬 알고리즘, 삽입 정렬 알고리즘 (둘다 2중 for loop 구조)
  6. O(2n)
    • 지수 시간
    • 입력 데이터의 크기에 따라 걸리는 시간은 2의 n 제곱만큼 비례
    • 보통 문제를 풀기 위한 모든 조합과 방법을 시도할 때 사용됨
    • 대표적 알고리즘: 피보나치 수열, 재귀가 역기능을 할 경우도 해당됨

성능 순서

[Excellent] O(1) < O(logn) < O(n) < O(n log n) < O(n2) < O(2n) [Horrible]
Big-O 성능 그래프

Big O 표기와 입력 데이터 크기에 따른 성능을 비교
| Big O 표기 | 10 개 일때 | 100 개 일때 | 1000 개 일때 |
|——|——|——|——|
| O(1) | 1 | 1 | 1 |
| O(log n) | 3 | 6 | 9 |
| O(n) | 10 | 100 | 1000 |
| O(n log n) | 30 | 600 | 9000 |
| O(n2) | 100 | 10000 | 1000000 |
| O(2n) | 1024 | 1.26e+29 | 1.07e+301 |
| O(N!) | 3628800 | 9.3e+157 | 4.02e+2567 |

Big-O 시간복잡도 계산

몇 가지 시간복잡도 Big-O 표기법을 예시로 계산법을 알아보도록 하겠습니다.

문제 1

1
2
3
4
5
6
function print(arg) {
  console.log(arg)
}

print('hello')
> "hello"

위 코드는 시간 복잡도: O(1) 인 코드로 실행되는 코드 라인은 print 함수 내부 console.log(arg) 뿐이다.

문제 2

1
2
3
4
5
6
7
8
9
10
11
function loop(n) {
  for(let i=0;i < n;i++){
    console.log(i);
  }
}

loop(10)
> 1
> 2
> ....
> 10

위 코드는 시간 복잡도: O(n) 인 코드로 실행되는 코드 라인은 loop 함수의 for loop가 n 번만큼 반복하기 떄문이다.

문제 2: 기출변형
1
2
3
4
5
6
7
8
9
10
function loop2(n) {
  for(let i=0;i<n;i++){
    console.log(i);
  }
  for(let i=0;i<n;i++){
    console.log(i);
  }
}

loop2(10)

위 코드 loop2 함수 내부에 loop 문이 2개 있지만 시간복잡도 계산에서는 영향이 가장 큰 알고리즘 하나만 계산하기 때문에 O(n2)가 아닌 시간 복잡도: O(n) 입니다.

문제 3

1
2
3
4
5
6
7
8
9
10
function looploop(n) {
  for(let i=0;i<n;i++){
    console.log(i);
    for(let j=0;j<n;j++){
      console.log(j);
    }
  }
}

looploop(10)

위 코드는 loop에 loop가 있는 이중 loop 문으로 시간 복잡도: O(n2) 입니다.

문제 3: 기출변형
1
2
3
4
5
6
7
8
9
10
11
12
function looploop2(n) {
  for(let i=0;i<n;i++){
    for(let j=i;j<n;j++{
      console.log(j);
    }
  }
  for(let i=0;i<n;i++){
    console.log(i);
  }
}

looploop2(10)

위 코드는 이중 loop문과 단수 loop이 있는 코드로써, ##### 문제 2: 기출변형 에서 언급했듯이 영향이 가장 큰 알고리즘만 시간복잡도에서는 계산하기 때문에 시간 복잡도: O(n2) 이다.

아래 문제는 아래의 데이터를 기반으로 풀어보겠습니다.

1
2
3
4
5
6
7
8
var attendance = {
  'Kim' : true,
  'Amili' : false,
  'Moon' : true,
  'Koon' :  true,
  'Joon' : true,
}
var attendanceAges = [21, 29, 22, 25, 27]
문제 4
1
2
3
4
5
6
function isAttendant (name) {
  return attendance[name]
}

isAttendant['Kim']
isAttendant['Moon']

위 코드는 isAttendant 함수에 name 인자를 넘겨 attendance 데이터에서 알고 있는 또는 전달받은 key 또는 index에 따라 결과값을 return 하는 함수로 시간 복잡도: O(1) 이다.

문제 5
1
2
3
4
5
6
7
8
9
function thisOld(num, array){
  var midPoint = Math.floor(array.length/2);
  if( array[midPoint] === num) return true;
  if( array[midPoint] < num ) // --> only look at second half of the array
  if( array[midpoint] > num ) // --> only look at first half of the array
  // recursively repeat until you arrive at your solution 
}

thisOld(28, attendanceAges)

위 코드는 이진탐색 트리 알고리즘으로, thisOld 함수에 인자로 array 배열과 num을 념겨주고 내부 함수에서는 함수의 결과값을 찾기 위해 array 인자를 계속 반으로 분할하면서 값을 탐색하기 떄문에 배열에서 어느 방향으로 탐색을 시작할지 알고 있으면 탐색시간이 두배로 줄어든다. 따라서 시간 복잡도: O(log n) 인 알고리즘이다.

시간복잡도 줄이는 법

일단 시간복잡도를 줄이는 법을 많이 찾아봤지만 자료를 많이 찾아보진 못했고 몇몇 국내외 블로그에서 언급 됐던 것은 아래와 같습니다.

  1. 알고리즘에서 시간복잡도에 가장 큰 영향을 끼치는 것은 반복문 이다.
    • #문제1 ~ 3 이 반복문이 시간복잡도를 올리는 그 예이다.
  2. 해결해야할 문제 또는 이슈에 맞는 적절한 알고리즘을 설계하라.
    • 알고리즘마다 핸들링 가능한 적절한 문제해결 케이스가 있기 때문에 외워두고 있거나 참고자료를 참고한다면 시간복잡도를 낮출 수 있다.
  3. 각 알고리즘의 형태에 맞는 효율적인 자료구조 들을 이용한다면 시간 복잡도를 낮출 수 있다.
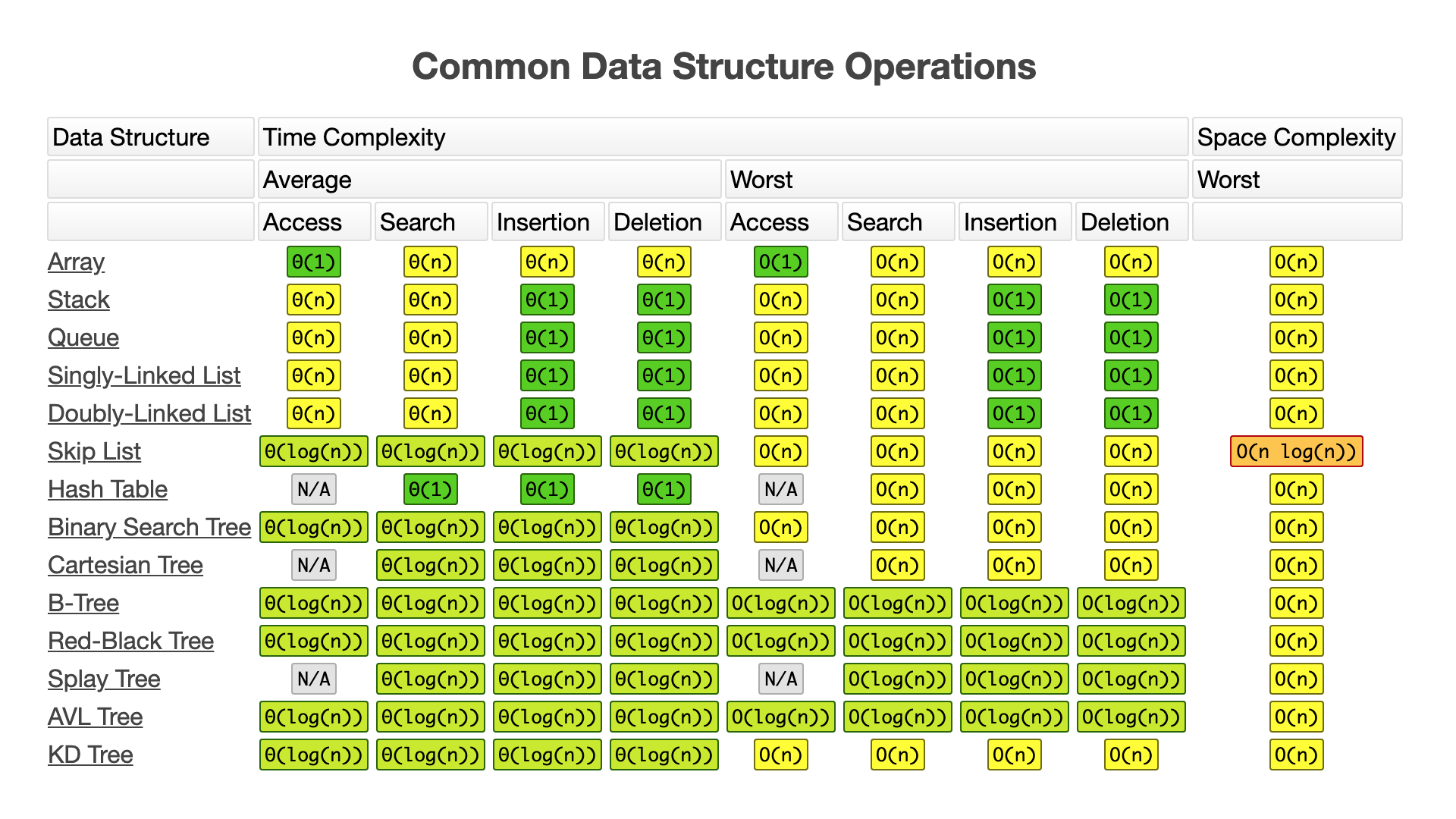
    Common Data Structure Operations
    Array Sorting Algorithms

부록

자료구조 작업별 복잡도

자료 구조 접근 검색 삽입 삭제 비고
배열 1 n n n
스택 n n 1 1
큐 n n 1 1
연결 리스트 n n 1 1
해시 테이블 - n n n 완벽한 해시 함수의 경우 O(1)
이진 탐색 트리 n n n n 균형 트리의 경우 O(log(n))
B-트리 log(n) log(n) log(n) log(n)
Red-Black 트리 log(n) log(n) log(n) log(n)
AVL 트리 log(n) log(n) log(n) log(n)
Bloom Filter - 1 1 - 거짓 양성이 탐색 중 발생 가능

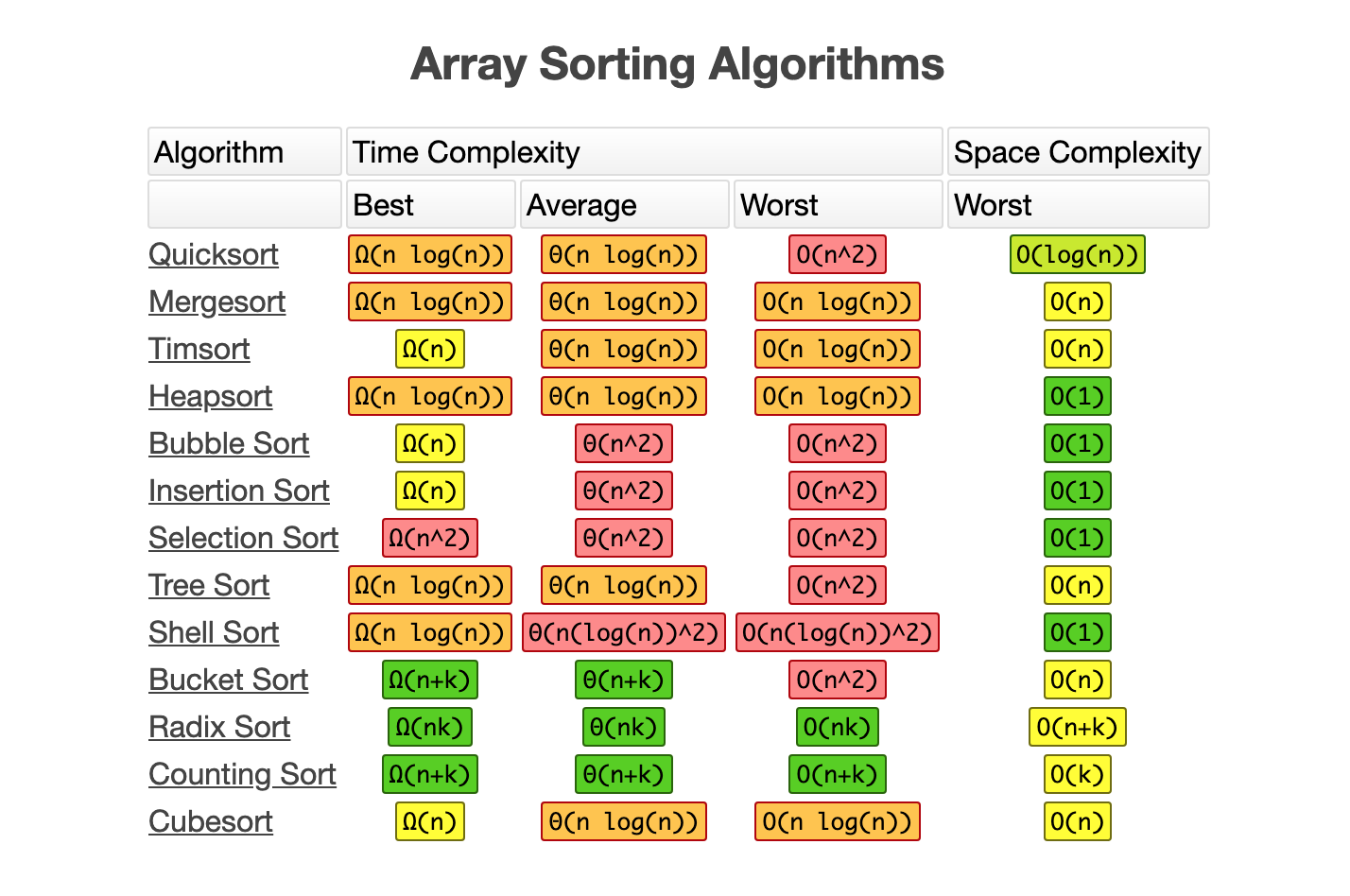
정렬 알고리즘 복잡도

이름 최적 평균 최악 메모리 동일값 순서 유지 비고
거품 정렬 n n2 n2 1 Yes
삽입 정렬 n n2 n2 1 Yes
선택 정렬 n2 n2 n2 1 No
힘 정렬 n log(n) n log(n) n log(n) 1 No
병합 정렬 n log(n) n log(n) n log(n) n Yes
퀵 정렬 n log(n) n log(n) n2 log(n) No 보통 제자리로 O(log(n))
스택공간으로 수행됨
셀 정렬 n log(n) n log(n) n (log(n))2 1 No
계수 정렬 n + r n + r n + r n + r Yes r - 배열내 가장 큰 수
기수 정렬 n * k n * k n * k n * k n + k Yes

참고

Share